-
강한 연결 요소(SCC, Strongly Connected Component)Algorithm/이론 2020. 12. 2. 21:21
강한 연결 요소(SCC, Strongly Connected Component)
- 방향이 있는 그래프에서 다음 조건을 만족하는 부분집합
- (1) SCC 내부의 임의의 정점 u, v는 직, 간접적으로 서로 도달이 가능하다.
- (2) SCC 내부의 정점과 외부의 정점끼리는 서로 이어진 경로가 존재하지 않는다.
- SCC는 Maximal한 성질을 가지고 있어 형성될 수 있는 가장 큰 집합으로 형성된다.
- SCC를 추출하는 대표적인 알고리즘은 코사라주 알고리즘(구현이 쉬움)과 타잔 알고리즘(적용이 쉬움)이 있다.
필요한 자료구조 & 변수
변수 설명 List<List<Integer>> graph, reverseGraph 정방향 & 역방향 그래프 int[] visited 방문 여부 체크 배열 Stack<Integer> stack DFS 호출 시작점을 찾기위한 stack List<List<Integer>> SCC SCC 집합 저장 그래프 Flow
1. graph와 reverseGraph에 그래프 연결 정보를 저장한다.
2. for(V, 모든 정점)으로 인접 정점에 대해 방문 체크를하고 DFS로 연결이 끝나는 지점까지 들어간다.
그리고 DFS 호출이 끝나는 시점에 stack에 push한다. -> LIFO 구조로 처음 호출한 노드가 가장 위로 올라오기 때문
3. 다시 visited 배열을 초기화 한 후,
while(!stack.isEmpty())으로 reverseGraph로 reDFS 호출을 한다.
이때, 1번 로직에서의 DFS와 달라지는 점은 노드를 SCC에 추가하여 SCC 집합을 만드는 것
소스코드
2150번: Strongly Connected Component
첫째 줄에 두 정수 V(1 ≤ V ≤ 10,000), E(1 ≤ E ≤ 100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정
www.acmicpc.net
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115import java.io.BufferedReader;import java.io.IOException;import java.io.InputStreamReader;import java.util.*;public class Main {static int V, E;static List<List<Integer>> graph, reverseGraph, SCC;static boolean[] visited;static Stack<Integer> stack;public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));StringTokenizer st = new StringTokenizer(br.readLine());V = stoi(st.nextToken());E = stoi(st.nextToken());graph = new ArrayList<>();reverseGraph = new ArrayList<>();SCC = new ArrayList<>();stack = new Stack<>();visited = new boolean[V + 1];for (int i = 0; i < V + 1; i++) {graph.add(new ArrayList<>());reverseGraph.add(new ArrayList<>());}// inputint from, to;for (int i = 0; i < E; i++) {st = new StringTokenizer(br.readLine());from = stoi(st.nextToken());to = stoi(st.nextToken());graph.get(from).add(to);reverseGraph.get(to).add(from);}// (1)for (int i = 1; i <= V; i++) {if (!visited[i]) {// (2)DFS(i);}}Arrays.fill(visited, false);// (3)int sccNum = 0;SCC.add(new ArrayList<>());while (!stack.isEmpty()) {int node = stack.pop();if (!visited[node]) {reDFS(node, sccNum);sccNum++;SCC.add(new ArrayList<>());}}SCC.remove(SCC.size() - 1);for (List<Integer> s : SCC) {Collections.sort(s);}// SCC 정렬Collections.sort(SCC, new Comparator<List<Integer>>() {@Overridepublic int compare(List<Integer> o1, List<Integer> o2) {return o1.get(0) - o2.get(0);}});// outputStringBuilder sb = new StringBuilder();sb.append(SCC.size());sb.append('\n');for (List<Integer> s : SCC) {for (int i : s) {sb.append(i + " ");}sb.append(-1);sb.append('\n');}System.out.println(sb.toString());}private static void reDFS(int node, int sccNum) {visited[node] = true;SCC.get(sccNum).add(node);for (int i : reverseGraph.get(node)) {if (!visited[i]) {reDFS(i, sccNum);}}}private static void DFS(int node) {visited[node] = true;for (int i : graph.get(node)) {if (!visited[i]) {DFS(i);}}stack.push(node);}private static int stoi(String s) {return Integer.parseInt(s);}}cs 결과
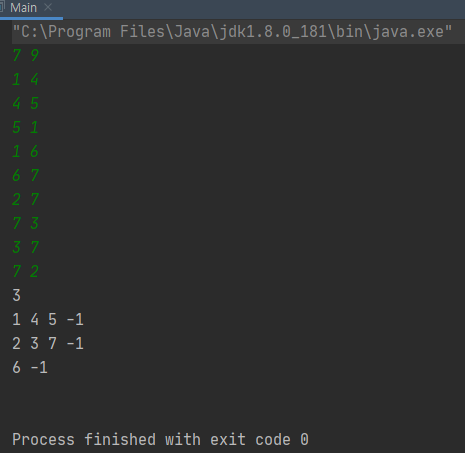
참고자료
'Algorithm > 이론' 카테고리의 다른 글
위상 정렬(Topological Sort) (1) 2020.11.29 다익스트라 알고리즘(Dijkstra's Algorithm) (0) 2020.08.25 이분 탐색 (Binary Search) (0) 2020.04.24 누적합(Cumulative sum) 2 (0) 2020.04.14 누적합(Cumulative sum) (0) 2020.04.14